Սա կարող է համարվել Հովհաննես Դավթյանի տեսության տեխնիկակակն մասի լաբորատոր առաջին ապացույցը՝ մեզ այսօր հասկանալի նյութական կամ էներգետիկ կրիչների բացակայության դեքում տեղեկատվության փոխանցման հնարավորությունը:
- Yuan Caoa,b,1,
- Yu-Huai Lia,b,1,
- Zhu Caoc,
- Juan Yina,b,
- Yu-Ao Chena,b,
- Hua-Lei Yina,b,
- Teng-Yun Chena,b,
- Xiongfeng Mac,
- Cheng-Zhi Penga,b,2, and
- Jian-Wei Pana,b,2
Direct counterfactual communication via quantum Zeno effect
Yuan Cao, Yu-Huai Li, Zhu Cao, Juan Yin, Yu-Ao Chen, Hua-Lei Yin, Teng-Yun Chen, Xiongfeng Ma, Cheng-Zhi Peng, and Jian-Wei Pan
See all authors and affiliations
PNAS May 9, 2017 114 (19) 4920-4924; first published April 25, 2017; https://doi.org/10.1073/pnas.1614560114
- Edited by Gilles Brassard, Université de Montréal, Montreal, Canada, and accepted by Editorial Board Member Anthony Leggett March 29, 2017 (received for review August 31, 2016)
Significance
Recent theoretical studies have shown that quantum mechanics allows counterfactual communication, even without actual transmission of physical particles, which raised a heated debate on its interpretation. Although several papers have been published on the theoretical aspects of the subject, a faithful experimental demonstration is missing. Here, by using the quantum Zeno effect and a single-photon source, direct communication without carrier particle transmission is implemented successfully. We experimentally demonstrate the feasibility of direct counterfactual communication with the current technique. The results of our work can help deepen the understanding of quantum mechanics. Furthermore, our experimental scheme is applicable to other quantum technologies, such as imaging and state preparation.
Abstract
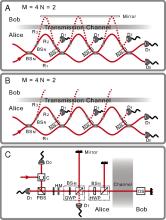
Intuition from our everyday lives gives rise to the belief that information exchanged between remote parties is carried by physical particles. Surprisingly, in a recent theoretical study [Salih H, Li ZH, Al-Amri M, Zubairy MS (2013) Phys Rev Lett 110:170502], quantum mechanics was found to allow for communication, even without the actual transmission of physical particles. From the viewpoint of communication, this mystery stems from a (nonintuitive) fundamental concept in quantum mechanics—wave-particle duality. All particles can be described fully by wave functions. To determine whether light appears in a channel, one refers to the amplitude of its wave function. However, in counterfactual communication, information is carried by the phase part of the wave function. Using a single-photon source, we experimentally demonstrate the counterfactual communication and successfully transfer a monochrome bitmap from one location to another by using a nested version of the quantum Zeno effect.
See all authors and affiliations
PNAS May 9, 2017 114 (19) 4925-4929; first published April 25, 2017; https://doi.org/10.1073/pnas.1618780114
- Contributed by Drew Fudenberg, March 27, 2017 (sent for review November 14, 2016; reviewed by Keisuke Hirano, Demian Pouzo, and Bruno Strulovici)
Significance
Many decision problems in contexts ranging from drug safety tests to game-theoretic learning models require Bayesian comparisons between the likelihoods of two events. When both events are arbitrarily rare, a large data set is needed to reach the correct decision with high probability. The best result in previous work requires the data size to grow so quickly with rarity that the expectation of the number of observations of the rare event explodes. We show for a large class of priors that it is enough that this expectation exceeds a prior-dependent constant. However, without some restrictions on the prior the result fails, and our condition on the data size is the weakest possible.
Abstract
We study how much data a Bayesian observer needs to correctly infer the relative likelihoods of two events when both events are arbitrarily rare. Each period, either a blue die or a red die is tossed. The two dice land on side 1 with unknown probabilities p1 and q1, which can be arbitrarily low. Given a data-generating process where p1≥cq1, we are interested in how much data are required to guarantee that with high probability the observer’s Bayesian posterior mean for p1 exceeds (1−δ)c times that for q1. If the prior densities for the two dice are positive on the interior of the parameter space and behave like power functions at the boundary, then for every ϵ> 0, there exists a finite N so that the observer obtains such an inference after n periods with probability at least 1−ϵ whenever np1≥N. The condition on n and p1 is the best possible. The result can fail if one of the prior densities converges to zero exponentially fast at the boundary.
Suppose a physician is deciding between a routine surgery and a newly approved drug for her patient. Either treatment can, in rare cases, lead to a life-threatening complication. She adopts a Bayesian approach to estimate the respective probability of complication, as is common among practitioners in medicine when dealing with rare events; see, for example, refs. 1 and 2 on the “zero-numerator problem.” She reads the medical literature to learn about n patient outcomes associated with the two treatments and chooses the new drug if and only if her posterior mean regarding the probability of complication due to the drug is lower than (1−δ) times that of the surgery. As the true probability of complication becomes small for both treatments, how quickly does n need to increase to ensure that the physician will correctly choose surgery with probability at least 1−ϵ when surgery is in fact the safer option?
Phrased more generally, we study how much data are required for the Bayesian posterior means on two probabilities to respect an inequality between them in the data-generating process, where these true probabilities may be arbitrarily small. Each period, one of two dice, blue or red, is chosen to be tossed. The choices can be deterministic or random, but have to be independent of past outcomes. The blue and red dice land on side k with unknown probabilities pk and qk, and the outcomes of the tosses are independent of past outcomes. Say that the posterior beliefs of a Bayesian observer satisfy (c,δ) monotonicity for side k¯ if his posterior mean for pk¯ exceeds (1−δ)c times that for qk¯ whenever the true probabilities are such that pk¯≥cqk¯. We assume the prior densities are continuous and positive on the interior of the probability simplex and behave like power functions at the boundary. Then we show that, under a mild condition on the frequencies of the chosen colors, for every ϵ> 0, there exists a finite N so that the observer holds a (c,δ)-monotonic belief after n periods with probability at least 1−ϵ whenever npk¯≥N. This condition means that the expected number of times the blue die lands on side k¯ must exceed a constant that is independent of the true parameter. Examples show that the sample size condition is the best possible and that the result can fail if one of the prior densities converges to zero exponentially fast at the boundary. A crucial aspect of our problem is the behavior of estimates when the true parameter value approaches the boundary of the parameter space, a situation that is rarely studied in a Bayesian context.
Suppose that in every period, the blue die is chosen with the same probability and that outcome k¯ is more likely under the blue die than under the red one. Then, under our conditions, an observer who sees outcome k¯ but not the die color is very likely to assign a posterior odds ratio to blue vs. red that is not much below the prior odds ratio. That is, the observer is unlikely to update her beliefs in the wrong direction. This corollary is used in ref. 3 to provide a learning-based foundation for equilibrium refinements in signaling games.
The best related result known so far is a consequence of the uniform consistency result of Diaconis and Freedman in ref. 4. Their result leads to the desired conclusion only under the stronger condition that the sample size is so large that the expected number of times the blue die lands on side k¯ exceeds a threshold proportional to 1/pk¯. That is, the threshold obtained from their result explodes as pk¯ approaches zero.
Our improvement of the sample size condition is made possible by a pair of inequalities that relate the Bayes estimates to observed frequencies. Like the bounds of ref. 4, the inequalities apply to all sample sequences without exceptional null sets and they do not involve true parameter values. Our result is related to a recent result of ref. 5, which shows that, under some conditions, the posterior distribution converges faster when the true parameter is on the boundary. Our result is also related to ref. 6, which considers a half space not containing the maximum-likelihood estimate of the true parameter and studies how quickly the posterior probability assigned to the half space converges to zero.
Bayes Estimates for Multinomial Probabilities
We first consider the simpler problem of estimating for a single K-sided die the probabilities of landing on the various sides. Suppose the die is tossed independently n times. Let Xkn denote the number of times the die lands on side k. Then Xn=(X1n,…,XKn) has a multinomial distribution with parameter n∈ℕ and unknown parameter p=(p1,…,pK)∈Δ, where ℕ is the set of positive integers and Δ={p∈[0,1]K:p1+…+pK= 1}. Let ℕ0=ℕ∪{0}. Let π be a prior density on Δ with respect to the Lebesgue measure λ on Δ, normalized by λ(Δ)= 1/(K− 1)!. Let π(⋅|Xn) be the posterior density after observing Xn.
Motivated by applications where some of the pk can be arbitrarily small, we are interested in whether the relative error of the Bayes estimator p^k(Xn)=∫pkπ(p|Xn)dλ(p) is small with probability close to 1, uniformly on large subsets of Δ. Specifically, given k∈{1,…,K} and ϵ> 0, we seek conditions on n and p and the prior, so that
ℙp(|p^k(Xn)−pk|<pkϵ)≥1−ϵ.
[1]
A subscript on ℙ or ? indicates the parameter value under which the probability or expectation is to be taken.
For a wide class of priors, we show in Theorem 1 that there is a constant N that is independent of the unknown parameter so that [1] holds whenever ?p(Xkn)≥N. Denote the interior of Δ by int Δ.
Condition?:
We say that a density π on Δ satisfies Condition P(α), where α=(α1,…,αK)∈(0,∞)K, if
π(p)∏k=1Kpkαk−1
is uniformly continuous and bounded away from zero on int Δ. We say that π satisfies Condition P if there exists α∈(0,∞)K so that π satisfies Condition P(α).
For example, if K= 2, then π satisfies Condition P(α) if and only if π is positive and continuous on int Δ and the limit limpk→0π(p)/pkαk−1 exists and is positive for k=1,2. For every K≥ 2, every Dirichlet distribution has a density that satisfies Condition P. Note that Condition P does not require that the density is bounded away from zero and infinity at the boundary. The present assumption on the behavior at the boundary is similar to Assumption P of ref. 5.
Theorem 1.
The proofs of the results in this section are given in SI Appendix.
The proof of Theorem 1 uses bounds on the posterior means given in Proposition 1 below. These bounds imply that there is an N∈ℕ so that if npk≥N and the maximum-likelihood estimator 1nXkn is close to pk, then |p^k(Xn)−pk|<pkϵ. It follows from Chernoff’s inequality that the probability that 1nXkn is not close to pk is at most ϵ.
Inequality 2 shows a higher accuracy of the Bayes estimator p^k(Xn) when the true parameter pk approaches 0. To explain this fact in a special case suppose that K= 2 and the prior is the uniform distribution. Then p^k(Xn)=(Xkn+ 1)/(n+2) and the mean squared error of p^k(Xn) is [npk(1−pk)+(1−2pk)2]/(n+2)2, which converges to 0 like 1n when pk∈(0,1) is fixed and like 1n2 when pk=1n. Moreover, by Markov’s inequality, the probability in [2] is less than (npk+1)/(n2pk2ϵ2), so that in this case we can choose N= 2/ϵ3. In general, we do not have an explicit expression for the threshold N, but in Remark 2 we discuss the properties of the prior that have an impact on the N we construct in the proof.
Condition P allows the prior density to converge to zero at the boundary of Δ like a power function with an arbitrarily large exponent. The following example shows that the conclusion of Theorem 1 fails to hold for a prior density that converges to 0 exponentially fast.
Example 1:
Let K= 2, π(p)∝e−1/p1, and δ> 0. Then for every N∈ℕ, there exist p∈Δ and n∈ℕ with n12+δp1≥N so that
ℙp(|p^1(Xn)−p1|>p1)=1.
The idea behind this example is that the prior assigns very little mass near the boundary point where p1= 0, so if the true parameter p1 is small, the observer needs a tremendous amount of data to be convinced that p1 is in fact small. The prior density in our example converges to 0 at an exponential rate as p1→ 0, and it turns out that the amount of data needed so that p^1(Xn)/p1 is close to 1 grows quadratically in 1/p1. For every fixed N∈ℕ and δ> 0, the pairs (n,p1) satisfying the relation n12+δp1=N involve a subquadratic growth rate of n with respect to 1/p1. So we can always pick a small enough p1 such that the corresponding data size n is insufficient.
The next example shows that the sample size condition of Theorem 1, npk≥N, cannot be replaced by a weaker condition of the form ζ(n)pk≥N for some function ζ with lim supn→∞ζ(n)/n=∞. Put differently, the set of p for which [2] can be proved cannot be enlarged to a set of the form {p:pk≥ϕϵ(n)} with ϕϵ(n)=o(1/n).
Example 2:
Suppose π satisfies Condition P. Let ζ:ℕ→(0,∞) be so that lim supn→∞ζ(n)/n=∞. Then for every N∈ℕ, there exist p∈Δ and n∈ℕ with ζ(n)p1≥N so that
ℙp(|p^1(Xn)−p1|>p1)=1.
The following proposition gives fairly sharp bounds on the posterior means under the assumption that the prior density satisfies Condition P. The result is purely deterministic and applies to all possible sample sequences. The bounds are of interest in their own right and also play a crucial role in the proofs of Theorems 1 and 2.
Proposition 1.
Suppose π satisfies Condition P(α). Then for every ϵ> 0, there exists a constant γ> 0 such that
(1−ϵ)nk+αkn+γ≤∫pk(∏i=1Kpini)π(p)dλ(p)∫(∏i=1Kpini)π(p)dλ(p)≤(1+ϵ)nk+γn+γ
[3]
for k= 1,…,K and all n,n1,…,nK∈ℕ0 with ∑i=1Kni=n.
Remark 1:
If π is the density of a Dirichlet distribution with parameter α∈(0,∞)K, then the inequalities in [3] hold with ϵ= 0 and γ=∑k=1Kαk, and the inequality on the left-hand side is an equality. If π is the density of a mixture of Dirichlet distributions and the support of the mixing distribution is included in the interval [a,A]K, 0≤a≤A<∞, then for all k and n1,…,nK with ∑i=1Kni=n,
nk+an+KA≤∫pk(∏i=1Kpini)π(p)dλ(p)∫(∏i=1Kpini)π(p)dλ(p)≤nk+An+Ka.
[4]
The proofs of our main results, Theorems 1 and 2, apply to all priors whose densities satisfy inequalities 3 or 4. In particular, the conclusions of these theorems and of their corollaries hold if the prior distribution is a mixture of Dirichlet distributions and the support of the mixing distribution is bounded.
Remark 2:
Condition P(α) implies that the function π(p)/∏k=1Kpkαk−1, p∈intΔ, can be extended to a continuous function π∼(p) on Δ. The proof of Proposition 1 relies on the fact that π∼ can be uniformly approximated by Bernstein polynomials. An inspection of the proof shows that the constant γ in [3] can be taken to be m+∑k=1Kαk, where m is so large that hm, the mth-degree Bernstein polynomial of π∼, satisfies
max{|hm(p)−π∼(p)|:p∈Δ}≤min{π∼(p):p∈Δ}1+2ϵ−1.
Hence, in addition to a small value of ϵ, the following properties of the density π result in a large value of γ: (i) if ∑k=1Kαk is large, (ii) if π is a “rough” function so that π∼ is hard to approximate and m needs to be large, and (iii) if π∼ is close to 0 somewhere. The threshold N in Theorem 1 depends on the prior through the constant γ from Proposition 1 and the properties of π just described will also lead to a large value of N.
In particular, N→∞ if ∑k=1Kαk→∞. For example, consider a sequence of priors π(j) for K= 2, where π(j) is the density of the Dirichlet distribution with parameter (j,1), so that π(j) satisfies Condition P(α) with α1=j. As j→∞, π(j) converges faster and faster to 0 as p1→ 0, although never as fast as in Example 1, where no finite N can satisfy the conclusion of Theorem 1. If n= 4j and p1=112, then under π(j), p^1(Xn)=(X1n+j)/(n+j+1)≥ 2p1, so for every ϵ∈(0,1), the probability in Theorem 1 is 1. Thus, the smallest N for which the conclusion holds must exceed 4j×112=j3.
Remark 3:
Using results on the degree of approximation by Bernstein polynomials, one may compute explicit values for the constants γ in Proposition 1 and N in Theorem 1. Details are given in in SI Appendix, Remarks 3′ and 3″.
Remark 4:
Suppose K> 2 and the statistician is interested in only one of the probabilities pk, say pk¯. Then, instead of using p^k¯(Xn), he may first reduce the original (K− 1)-dimensional estimation problem to the problem of estimating the one-dimensional parameter (pk¯,∑k≠k¯pk) of the Dirichlet distribution of (Xk¯n,∑k≠k¯Xkn). He will then distinguish only whether or not the die lands on side k¯ and will use the induced one-dimensional prior distribution for the parameter of interest. If the original prior is a Dirichlet distribution on Δ, both approaches lead to the same Bayes estimators for pk¯, but in general, they do not. SI Appendix, Proposition 2 shows that whenever the original density π satisfies Condition P, then the induced density satisfies Condition P as well. However, it may happen that the induced density satisfies Condition P even though the original density does not. For example, if K= 3 and π(p)∝e−1/p1+p2, then π does not satisfy Condition P, but for each k¯= 1,2,3, the induced density does.
Comparison of Two Multinomial Distributions
Here we consider two dice, blue and red, each with K≥ 2 sides. In every period, a die is chosen. We first consider the case where the choice is deterministic and fixed in advance. We later allow the choice to be random. The chosen die is tossed and lands on the kth side according to the unknown probability distributions p=(p1,…,pK) and q=(q1,…,qK) for the blue and the red die, respectively. The outcome of the toss is independent of past outcomes. The parameter space of the problem is Δ2. The observer’s prior is represented by a product density π(p)ϱ(q) over Δ2; that is, he regards the parameters p and q as realizations of independent random vectors.
Let Xn be a random vector that describes the outcomes, i.e., colors and sides, of the first n tosses. Let bn denote the number of times the blue die is tossed in the first n periods. Let π(⋅|Xn) and ϱ(⋅|Xn) be the posterior densities for the blue and the red die after observing Xn. Let p^k(Xn)=∫pkπ(p|Xn)dλ(p) and q^k(Xn)=∫qkϱ(q|Xn)dλ(q). The product form of the prior density ensures that the marginal posterior distribution for either die is completely determined by the observations on that die and the marginal prior for that die.
We study the following problem. Fix a side k¯∈{1,…,K} and a constant c∈(0,∞). Consider a family of environments, each characterized by a data-generating parameter vector ϑ=(p,q)∈Δ2 and an observation length n. In each environment, we have pk¯≥cqk¯, and we are interested in whether the Bayes estimators reflect this inequality. In general, one cannot expect that the probability that p^k¯(Xn)≥cq^k¯(Xn) is much higher than 12 when pk¯=cqk¯. We therefore ask whether in all of the environments, the observer has a high probability that p^k¯(Xn)≥c(1−δ)q^k¯(Xn) for a given constant δ∈(0,1).
Clearly, as pk¯ approaches 0, we will need a larger observation length n for the data to overwhelm the prior. But how fast must n grow relative to pk¯? Applying the uniform consistency result of ref. 4 to each Bayes estimator separately leads to the condition that n must be so large that the expected number of times the blue die lands on side k¯, that is, bnpk¯, exceeds a threshold that explodes when pk¯ approaches zero. The following theorem shows that there is a threshold that is independent of p, provided the prior densities satisfy Condition P.
Theorem 2.
Suppose that π and ϱ satisfy Condition P. Let k¯∈{1,…,K}, c∈(0,∞), and ϵ,δ,η∈(0,1). Then there exists N∈ℕ so that for every deterministic sequence of choices of the dice to be tossed,
ℙϑ(p^k¯(Xn)≥c(1−δ)q^k¯(Xn))≥1−ϵ
[5]
for all ϑ=(p,q)∈Δ2 with pk¯≥cqk¯ and all n∈ℕ with bnpk¯≥N and bn/n≤ 1−η.
We prove Theorem 2 in the next section.
Note that the only constraints on the sample size here are that the product of bn with pk¯ be sufficiently large and the proportion of periods in which the red die is chosen be not too small. However, pk¯ and qk¯ can be arbitrarily small. This is useful in analyzing situations where the data-generating process contains rare events.
In the language of hypothesis testing, Theorem 2 says that under the stated condition on the prior, the test that rejects the null hypothesis pk¯≥cqk¯ if and only if p^k¯(Xn)<c(1−δ)q^k¯(Xn) has a type I error probability of at most ϵ provided pk¯≥N/bn (and bn/n< 1−η). For every n, the bound on the error probability holds uniformly on the specified parameter set. Note that such a bound cannot be obtained for a test that rejects the hypothesis whenever p^k¯(Xn)<cq^k¯(Xn).
We now turn to the case where the dice are randomly chosen. The probability of choosing the blue die need not be constant over time but must not depend on the unknown parameter ϑ. Let the random variable Bn denote the number of times the blue die is tossed in the first n periods.
Corollary 1.
Suppose that π and ϱ satisfy Condition P. Let k¯∈{1,…,K}, c∈(0,∞), and ϵ,δ∈(0,1). Suppose that in every period, the die to be tossed is chosen at random, independent of the past, and that
lim infn→∞?(Bn)n>0, lim supn→∞?(Bn)n<1.
[6]
Then there exists N∈ℕ so that
ℙϑ(p^k¯(Xn)≥c(1−δ)q^k¯(Xn))≥1−ϵ
[7]
for all ϑ=(p,q)∈Δ2 with pk¯≥cqk¯ and all n∈ℕ with npk¯≥N.
The proof of Corollary 1 is given at the end of the next section.
In the decision problem described at the beginning, Theorem 2 and Corollary 1 ensure that whenever surgery is the safer option, the probability that the physician actually chooses surgery is at least 1−ϵ unless the probability of complication due to the drug is smaller than N/n. Except for this last condition, the bound 1−ϵ holds uniformly over all possible parameters.
In the rest of this section we assume that in every period the blue die is chosen at random with the same probability μB. The value of μB need not be known; we assume only that 0<μB< 1, so that condition 6 is met.
The following example shows that the conditions on the prior densities cannot be omitted from Corollary 1.
Example 3:
Suppose K= 2 and 0<μB< 1. Suppose π satisfies Condition P and ϱ(q)∝e−1/q1. Let c> 0. Then for every N∈ℕ, there exist ϑ=(p,q)∈Δ2 with p1≥cq1 and n∈ℕ with np1≥N so that
ℙϑ(p^1(Xn)<c2q^1(Xn))>12.
The next example shows that the sample size condition of Corollary 1, npk¯≥N, is the best possible for small pk¯. It cannot be replaced by a weaker condition of the form nζ(pk¯)≥N for some function ζ with limt→0+ζ(t)/t=∞. In particular, taking ζ to be a constant function shows that there does not exist N∈ℕ so that n≥N implies that [7] holds uniformly for all ϑ with pk≥cqk.
Example 4:
Suppose that 0<μB< 1 and that π and ϱ satisfy Condition P. Let c> 0. Let ζ be a nonnegative function on [0,1] with limt→0+ζ(t)/t=∞. Then there exists ϵ0> 0 so that for every N∈ℕ, there exist ϑ=(p,q)∈Δ2 with p1≥cq1 and n∈ℕ with nζ(p1)≥N so that
ℙϑ(p^1(Xn)<c2q^1(Xn))>ϵ0.
Examples 3 and 4 are proved in SI Appendix.
Suppose that after data Xn the observer was told that the next outcome was k¯ but not which die was used. Then Bayes’ rule implies the posterior odds ratio for “blue” relative to “red” is
μB∫pk¯π(p|Xn)dλ(p)μR∫qk¯ϱ(q|Xn)dλ(q),
where μR= 1−μB.
Corollary 2.
Suppose that π and ϱ satisfy Condition P. Then there exists N∈ℕ such that whenever pk¯≥qk¯ and npk¯≥N, there is probability at least 1−ϵ that the posterior odds ratio of blue relative to red exceeds (1−ϵ)⋅μBμR when the (n+1)th die lands on side k¯.
Corollary 2 is used by Fudenberg and He in ref. 3, who provide a learning-based foundation for equilibrium refinements in signaling games. They consider a sequence of learning environments, each containing populations of blue senders, red senders, and receivers. Senders are randomly matched with receivers each period and communicate using one of K messages. There is some special message k¯, whose probability of being sent by blue senders always exceeds the probability of being sent by red senders in each environment. Suppose the common prior of the receivers satisfies Condition P and, in every environment, there are enough periods that the expected total observations of blue sender playing k¯ exceed a constant. Then at the end of every environment, by Corollary 2 all but ϵ fraction of the receivers will assign a posterior odds ratio for the color of the sender not much less than the prior odds ratio of red vs. blue, if they were to observe another instance of k¯ sent by an unknown sender, regardless of how rarely the message k¯ is observed. A leading case of receiver prior satisfying Condition P is fictitious play, the most commonly used model of learning in games, which corresponds to Bayesian updating from a Dirichlet prior, but Corollary 2 shows that the Dirichlet restriction can be substantially relaxed.
Proofs of Theorem 2 and Corollary 1
We begin with two auxiliary results needed in the proof of Theorem 2. Lemma 1 is a large deviation estimate that gives a bound on the probability that the frequency of side k¯ in the tosses of the red die exceeds an affine function of the frequency of side k¯ in the tosses of the blue die. Lemma 2 implies that, with probability close to 1, the number of times the blue die lands on side k¯ exceeds a given number when bnpk¯ is sufficiently large. The proofs of Lemmas 1 and 2 are in SI Appendix.
Lemma 1.
Let Sn be a binomial random variable with parameters n and p, and let Tm be a binomial random variable with parameters m and q. Let 0<c′<c and d> 0. Suppose Sn and Tm are independent, and p≥cq. Then
ℙ(Tmm≥1c′Snn+dn∧m)≤(c′c)c′d/(c′+1).
Lemma 2.
Let M<∞ and ϵ> 0. Then there exists N∈ℕ so that if Sn is a binomial random variable with parameters n and p and np≥N, then
ℙp(Sn≤M)≤ϵ.
Proof of Theorem 2:
Let rn=n−bn be the number of times the red die is tossed in the first n periods. Let Yn and Zn be the respective number of times the blue and the red die land on side k¯. Choose β> 0 and c′∈(0,c) so that
1−β(1+β)(1−δ)>cc′+δ.
[8]
By Proposition 1, there exists γ> 0 so that for every n∈ℕ,
p^k¯(Xn)≥ϕ(bn,Yn),q^k¯(Xn)≤ψ(rn,Zn),
[9]
where
ϕ(b,y)=(1−β)yb+γ,ψ(r,z)=(1+β)z+γr.
Let d> 0 be so that the bound in Lemma 1 satisfies (c′/c)c′d/(c′+1)≤ϵ2.
We now show that for all b,r∈ℕ, y= 0,…,b, and z=0,…,r, the inequalities
zr<1c′yb+db∧r, 2cγc′δ<b<rη, y>M:=3c(d+γ)δη
[10]
imply that
ϕ(b,y)>c(1−δ)ψ(r,z).
[11]
It follows from the first and the third inequality in [10] that
ψ(r,z)<ψ(r,ryc′b+rdb∧r)=(1+β)(yc′b+db∧r+γr)≤(1+β)(yc′b+δM3bc).
Applying this result, inequality 8, twice the second, and finally the fourth inequality in [10] we get
ϕ(b,y)−c(1−δ)ψ(r,z)(1−δ)(1+β)>yb+γ(1−β(1−δ)(1+β)−cc′−cγc′b)−δM3b≥yb+γ(δ−δ2)−δM3b≥23bδ2M−δM3b=0,
proving [11].
Let N={n∈ℕ:bn/n≤ 1−η}, N1=⌈2cγ/(c′δ)⌉, and for every n∈N with bn≥N1 define the events
Fn={Znrn<1c′Ynbn+dbn∧rn},Gn={Yn>M}.
For all n∈N, bn<rn/η. Thus, if n∈N and bn≥N1, the implication [10] ⇒ [11] yields that
Fn∩Gn⊂{ϕ(bn,Yn)>c(1−δ)ψ(rn,Zn)}.
Therefore, by inequalities 9,
Fn∩Gn⊂{p^k¯(Xn)≥c(1−δ)q^k¯(Xn)}.
It follows from Lemma 1 and the definition of d that for every ϑ=(p,q) with pk¯≥cqk¯, ℙϑ(Fnc)≤ϵ2. By Lemma 2, there exists N2∈ℕ so that ℙϑ(Gnc)≤ϵ2 for all n with bnpk¯≥N2. Thus, if pk¯≥cqk¯, n∈N, and bnpk¯≥N:=max(N1,N2), then
ℙϑ(p^k¯(Xn)≥c(1−δ)q^k¯(Xn))≥ 1−ℙϑ(Fnc)−ℙϑ(Gnc)≥ 1−ϵ.
Note that N does not depend on the sequence of the choices of the dice. □
Remark 5:
If K= 2, then for every n≥ 1 and every fixed number of times the red die is chosen in the first n periods, the Bayes estimate of qk¯ can be shown to be an increasing function of the number of times the red die lands on side k¯. This fact can be combined with Theorem 1 to give an alternative proof of Theorem 2 for the case K= 2. The monotonicity result does not hold for K> 2 and our Proof of Theorem 2 does not use Theorem 1.
Proof of Corollary 1:
By Chebyshev’s inequality, [Bn−?(Bn)]/n converges in probability to 0. Thus, by condition 6, there exists η> 0 and N1∈ℕ so that the event Fn={η≤Bn/n≤ 1−η} has probability ℙ(Fn)≥ 1−ϵ2 for all n≥N1. By Theorem 2, there exists N2∈ℕ so that
ℙϑ(p^k¯(Xn)≥c(1−δ)q^k¯(Xn)|Bn=bn)≥1−ϵ2
for all ϑ=(p,q)∈Δ2 with pk¯≥cqk¯ and all n∈ℕ and bn∈{1,…,n} with ℙ(Bn=bn)> 0 and bnpk¯≥N2 and bn/n≤1−η. Let N=max(N1,⌈N2/η⌉). Then for every ϑ with pk¯≥cqk¯ and every n∈ℕ with npk¯≥N, Fn⊂{Bnpk¯≥N2,Bn/n≤1−η}, so that
ℙϑ(p^k¯(Xn)≥c(1−δ)q^k¯(Xn)|Fn)≥1−ϵ2,
which implies [7] because ℙ(Fn)≥ 1−ϵ2. □
Acknowledgments
We thank three referees for many useful suggestions. We thank Gary Chamberlain, Martin Cripps, Ignacio Esponda, and Muhamet Yildiz for helpful conversations. This research is supported by National Science Foundation Grant SES 1558205.